Quantum Mystery Solved – Scientists shed light on puzzling high-temperature superconductors

A recent study advances the understanding of high-temperature superconductivity in cuprates using an improved Hubbard model, paving the way for potential technological breakthroughs and demonstrating the effectiveness of classical computation in quantum research.

Flatiron Institute senior research scientist Xu Zhang and his team used Hubbard’s model to computationally recreate key features of superconductivity in materials called cups that have puzzled scientists for decades.

High-speed hover trains, long-distance power transmission without loss of energy, faster MRI scanners – all these amazing technological innovations could be within reach if we could develop a material that conducts electricity without any resistance, or “superconductors”, at a temperature Room approx.

In a paper recently published in the journal SciencesResearchers have announced major advances in our understanding of the origins of superconductivity at relatively high (though still very cold) temperatures. The results relate to a class of superconductors that have puzzled scientists since 1986, called cuprates.

“There was tremendous excitement when copper superconductors were discovered [in 1986]“I think it’s surprising to everyone that almost 40 years later, we still don’t fully understand why they do what they do,” says Xu Zhang, a senior research scientist at the Flatiron Institute’s Center for Computational Quantum Physics (CCQ).

Illustration showing how electrons, which can have an up or down spin, form a striped pattern in the Hubbard model. Recent advanced calculations using this model are helping scientists better understand a class of high-temperature superconductors called cuprates. Credit: Lucy Reading-Ekanda/Simmons Foundation

In the new paper, Zhang and his colleagues successfully recreate the superconductivity features of coppers using a simple model called the 2D Hubbard model, which treats the material as if it were electrons moving around a quantum chessboard. This breakthrough comes only a few years after the same researchers demonstrated the simplest version of this model could not perform such a feat. Such direct models could spark a deeper understanding of physics, says study co-author Ulrich Schulwock, a professor at the University of Munich.

“The idea in physics is to keep the model as simple as possible, because it’s hard enough in itself,” says Shuluk. “So we first studied the simplest version imaginable.”

Improvements to Hubbard’s model

In the new study, the researchers added to Hubbard’s 2D model the ability of electrons to make diagonal hops, like bishops in a game of chess. Using this modification and thousands of weeks of simulations on supercomputers, the researchers’ model was able to capture the superconductivity and several other key features of coppers that had previously been found in experiments. By showing that Hubbard’s modest model can describe the superconductivity of coppers, the authors demonstrate its value as a platform for understanding why and how superconductivity arises.

For most of the last century, physicists thought they understood why some materials are superconductive. They believed that superconductivity only existed at extremely low temperatures below minus 243 degrees Celsius (about 30 degrees above Absolute zero). These low temperatures require expensive cooling systems that use liquid helium.

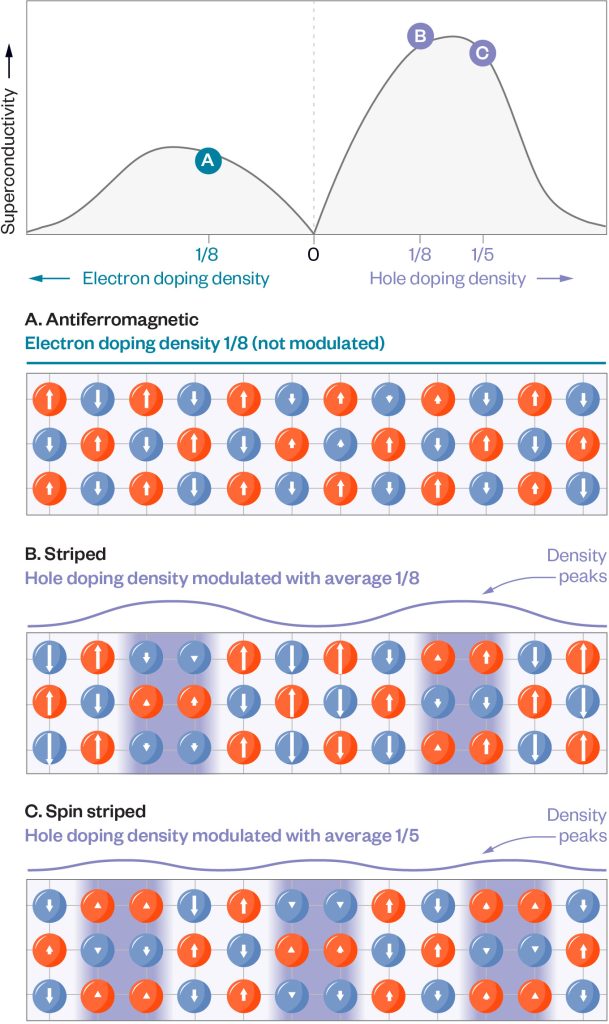
New research uses Hubbard’s two-dimensional model to study the emergence of superconductivity in a class of materials called cuprates. The model treats materials as electrons moving around a quantum chessboard, where each electron has an up or down spin. When there are the same number of electrons as there are on the checkerboard, the system forms a checkerboard pattern and is non-conductive. Adding electrons (in a process called electron grafting) or removing them (in a process called hole grafting after the empty positions left by the removed electrons) results in different levels of superconductivity (top panel). The bottom illustrations show the electron density or hole density as well as the spin patterns for three scenarios showing superconductivity. The first scenario (a) shows an antiferromagnetic checkerboard-like pattern of alternating up and down spins. The second (b) and third (c) scenarios show band patterns of spin and hole density variations. Credit: Lucy Reading-Ekanda/Simmons Foundation

When cuprates were discovered in 1986, they shocked the world of science by providing superconductivity at much higher temperatures. By the mid-1990s, scientists had discovered coppers that remained superconducting up to minus 123 degrees Celsius (about 150 degrees above absolute zero). These temperatures can be achieved using relatively cheap liquid nitrogen.

You can imagine cuprates as a lasagna of layers of copper oxide alternating with layers of other ions. (The name “cuprate” comes from the Latin word for copper.) Superconductivity is created when electricity flows without any resistance through layers of copper oxide. The simplest version of Hubbard’s 2D model uses just two terms to depict each layer as a checkerboard where electrons can jump north, south, east and west.

Complexity and computational challenges

“When I started working on the Hubbard model in the early days of high-temperature superconductivity, we thought that once we had the pure model simulated on a little ‘chessboard,’ we would fully understand superconductivity,” says study co-author Stephen White. “, a professor at the University of California, Irvine. “But as we developed the techniques, we found that Hubbard’s model was much more complex than we thought.”

Quantum mechanics creates this complexity: the layers are inhabited by electrons, each with an up or down spin. Electrons can become entangled. This entanglement means that electrons cannot be treated separately even when they are far apart, making them very difficult to simulate on a computer.

“Although Hubbard’s model can be written as an equation that takes only one or two lines of text, because it is applied to hundreds of atoms interacting through the strange laws of quantum mechanics, one can simulate it on a large computer the size of the Earth.” “For thousands of years we still haven’t been able to get the right answers,” White says.

Shortcuts are needed to deal with this level of complexity, and such shortcuts are the specialty of researchers. In the 1990s, White and Zhang separately developed now-famous techniques that significantly reduce computing time. To deal with the very complex pattern that comes from adding a diagonal jump, the researchers combined these two techniques. One technique holds that electrons are more like particles; The other emphasizes its wave structure.

“The important thing about this combination is that one is strong and the other is weak,” says Shuluk. “We can do a ‘handshake’ in a particular area where each works, authenticate one method using the other, and then explore the unknown where only one works.” Such a collaborative, multi-method approach is a legacy of the Simons collaboration on the multiple electron problem, which included several CCQ scientists, he says.

Besides the quantum mechanical rules of motion, the number of electrons on the chessboard affects the physics of the model. For many years, physicists have known that when there are the same number of electrons as there are spaces on the board, the electrons form a fixed checkerboard pattern of alternating up and down spins. This setup is not superconductive – in fact, it’s not conductive at all. Cuprates therefore require a change in the number of electrons.

In previous work by Zhang and colleagues using the simplest Hubbard model, adding or removing electrons did not lead to superconductivity. Instead, the stable checkerboard turned into a striped pattern, with lines consisting of either lines with extra electrons or lines with holes left by the removed electrons.

However, when the researchers added a diagonal jump factor to Hubbard’s model, the lines became only partially filled, and superconductivity emerged. Moreover, the results almost matched the experimental results regarding the properties of coppers.

“Do the lines strictly compete with superconductivity, or do they cause superconductivity, or is it something in between?” White asks. “The current answer is something in between, and is more complex than any of the other answers.”

Zhang says the research demonstrates the continued emergence of Hubbard’s model and “classical” computing, that is, the development of techniques and algorithms that make better use of regular computers, rather than waiting for quantum computers.

“After more than 30 years of intense community effort without many reliable answers, it is often said that a solution to the Hubbard model will have to wait for a quantum computer,” Zhang says. “This effort will not only advance research in the field of high-temperature superconductivity, but we also hope it will stimulate more research using ‘classical’ computation to explore the wonders of the quantum world.”

Reference: “Coexistence of superconductivity and partially filled lines in the Hubbard model” by Hao Xu, Chia-Min Chung, Mingpu Qin, Ulrich Schollwöck, Steven R. White and Shiwei Zhang, 10 May 2024, Sciences.
doi: 10.1126/science.adh7691