
Researchers have made a major advance in spectroscopic geometry by proving a special case of Bolya's conjecture relating to disk eigenvalues. Their work, which blends theoretical elegance with potential practical applications, highlights the universal value and artistic beauty of mathematical research. Credit: SciTechDaily.com
One of the professors and his collaborators proved Polya's conjecture about the eigenvalues of the disk, a difficult problem in mathematics.
Can the shape of the drum be deduced from the sounds it makes?
This is the kind of question that Iosif Poltrovic, a professor in the Department of Mathematics and Statistics at the University of Montreal, likes to ask. Poltrovic uses spectroscopic geometry, a branch of mathematics, to understand physical phenomena involving the propagation of waves.
A breakthrough in mathematical estimation
Last summer, Poltrović and his international collaborators – Nikolai Filonov, Michael Levitin, and David Scherr – proved a special case of the famous spectroscopic geometry conjecture formulated in 1954 by the eminent Hungarian-American mathematician George Polya.
The estimation concerns estimating the frequencies of the round cylinder, or, in mathematical terms, the eigenvalues of the disk.
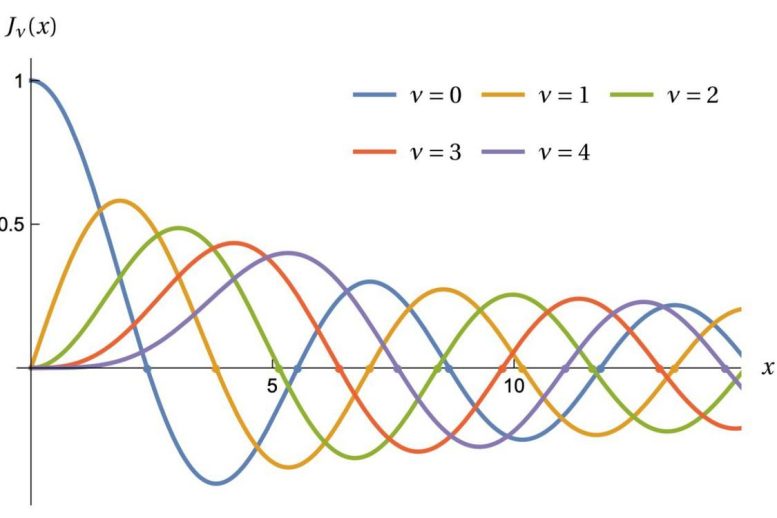
This diagram shows Bessel functions, where the dots correspond to the frequencies of the sounds produced by a round drum. Credit: Michael Levitin
Polya himself confirmed his conjecture in 1961 about the spheres that make up the plane, such as triangles and rectangles. Until last year, the guess was known only for these cases. The disc, despite its apparent simplicity, remained elusive.
“Imagine an infinite floor covered with tiles of the same shape that fit together to fill the space,” Poltrovic said. “They can be tiled with squares or triangles, but not with discs. Discs are actually not a good shape for tiling.
The universality and impact of mathematics
In an article published in July 2023 in the sports magazine Mathematics inventionsThe researchers showed that Bolya's conjecture is correct for a disk, a case that is considered particularly difficult.
Although their results are mainly of theoretical value, their proof method has applications in computational mathematics and numerical computation. The authors are now investigating this approach.

Joseph Poltrovic
“Although mathematics is a basic science, it is similar to sports and the arts in some ways,” Poltrovic said.
“Trying to prove a long-standing conjecture is a sport. Finding an elegant solution is an art. In many cases, beautiful mathematical discoveries are useful, you just have to find the right application.”
Reference: “The Polya Conjecture for Euclidean Spheres” by Nikolai Filonov, Michael Levitin, Iosif Poltrovic, and David A. Share, June 5, 2023, Mathematical inventions.
doi: 10.1007/s00222-023-01198-1

“Typical beer advocate. Future teen idol. Unapologetic tv practitioner. Music trailblazer.”







More Stories
Boeing May Not Be Able to Operate Starliner Before Space Station Is Destroyed
How did black holes get so big and so fast? The answer lies in the darkness
UNC student to become youngest woman to cross space on Blue Origin